Türk Matematik Tarihi Arşivi

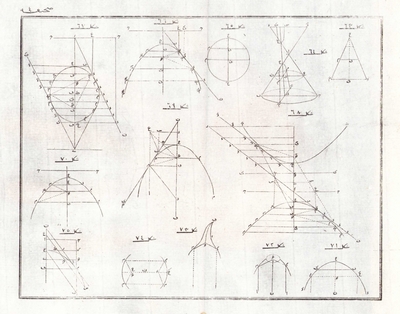
Başhoca İshak Efendi’nin dört ciltten oluşan dev eseri Mecmûa-i Ulûm-i Riyâziyye’nin birinci cildi tamamlanarak Sultan II. Mahmud’a sunuldu. Toplamda yaklaşık 2000 sayfayı bulan bu külliyat; aritmetik, cebir, geometri, koni kesitleri, diferansiyel ve integral hesap, mekanik, optik, elektrik, astronomi ve modern kimya gibi bilim dallarını kapsamaktadır . Eserin İstanbul baskısı 1831-1834 (Hicri 1247-1250) yılları arasında, Mısır (Bulak) baskısı ise 1841-1845 yılları arasında yapılmıştır. İshak Efendi bu eseri, Batı kaynaklarından (özellikle Fransızca) derleyip tercüme ederek ve kendi bilgilerini ekleyerek oluşturmuştur.

Mecmûa-i Ulûm-i Riyâziyye, Osmanlı bilim tarihinde Batı matematiğinin, özellikle de analizin (calculus) sistematik olarak aktarıldığı ilk ve en kapsamlı eserdir. Salih Zeki Bey'in tespitiyle, diferansiyel (hesab-ı tefāzulî) ve integral (hesab-ı tamâmî) hesap üzerine Türkçe yazılmış en eski metin olma özelliğini taşır. İshak Efendi, eserde integrali türevin tersi olarak tanımlamış, türev için ``lam'' harfine benzer özel bir işaret kullanırken, integral işlemi için "tam'' kelimesini sembolleştirmiştir. İntegral hesabını, $d(x^n)$ gibi temel ifadelerin ötesine taşıyarak alan hesaplamalarında (quadrature) etkin bir araç olarak kullanmıştır.

Eserin cebir bölümleri, Osmanlı matematiğinde karmaşık sayıların (complex numbers) ele alındığı öncü metinlerden biridir. İshak Efendi, $\sqrt{-1}$ ve $\sqrt{-4}$ gibi reel olmayan sayıları incelemiş, bunlara "kemmiyat-ı muhdese'' (sonradan ortaya çıkan veya uydurulmuş çokluklar) adını vermiştir. Bu sayıların dört işleme tabi tutulabileceğini göstererek, o dönem mühendislik eğitimi için şart olmasa da matematiksel bir merakla bu ileri kavramı literatüre kazandırmıştır.

Analitik geometri ve fonksiyonlar bahsinde de yenilikçi yaklaşımlar sergileyen İshak Efendi, logaritma kavramını detaylandırmış ve geometrik ortalamaları kullanarak $\log_{10} 9$ değerini 24 adımlı bir işlemle hassas bir şekilde hesaplamıştır. Daha da önemlisi, doğal logaritma fonksiyonu olan $\ln x$'i, bir hiperbol ile asimptotları arasında kalan alan olarak tanımlayarak modern analize hakimiyetini göstermiştir. Hiperbol üzerindeki çalışmaları sırasında, $x^2 - y^2 = b^2$ denklemiyle ifade edilen ikizkenar hiperbole, daireye benzer geometrik özelliklerinden dolayı "şibih-dā'ire'' (dairemsi) ismini vererek terminoloji üretimine de katkıda bulunmuştur.

Eser ayrıca, dönemin mühendislik müfredatının standartlarını aşan ileri düzey matematik problemlerini de barındırır. Matematik tarihinde Leibniz ve Bernoulli aileleri arasında tartışmalara yol açan meşhur "en kısa zaman eğrisi'' (brachistochrone) problemi ve bir eğrinin uzunluğunun integral yoluyla hesaplanması (rectification) gibi konular, eserde detaylıca çözülmüştür. İshak Efendi bu süreçte Batı terminolojisini Türkçeleştirmek için büyük çaba sarf etmiş, örneğin cissoide eğrisi için "münhani-yi sarmaşıkı'' terimini türetmiştir.

Arşiv Notu: Kaynaklarda eserin basım tarihi gün ve ay belirtilmeksizin Hicri 1247 yılı olarak geçmektedir. Hicri 1247 yılının başlangıcı (1 Muharrem) Miladi takvimde 12 Haziran 1831 tarihine tekabül ettiğinden, kesin basım gününün bilinmediği durumlarda uygulanan usul gereği dönemin başlangıç tarihi esas alınmıştır.

Kaynaklar:
1) Cem Tezer, Başhoca İshak Efendi ve Mecmu'a-yı Ulum-ı Riyaziye